Полезные материалы по Data Science и машинному обучению: 2 часть

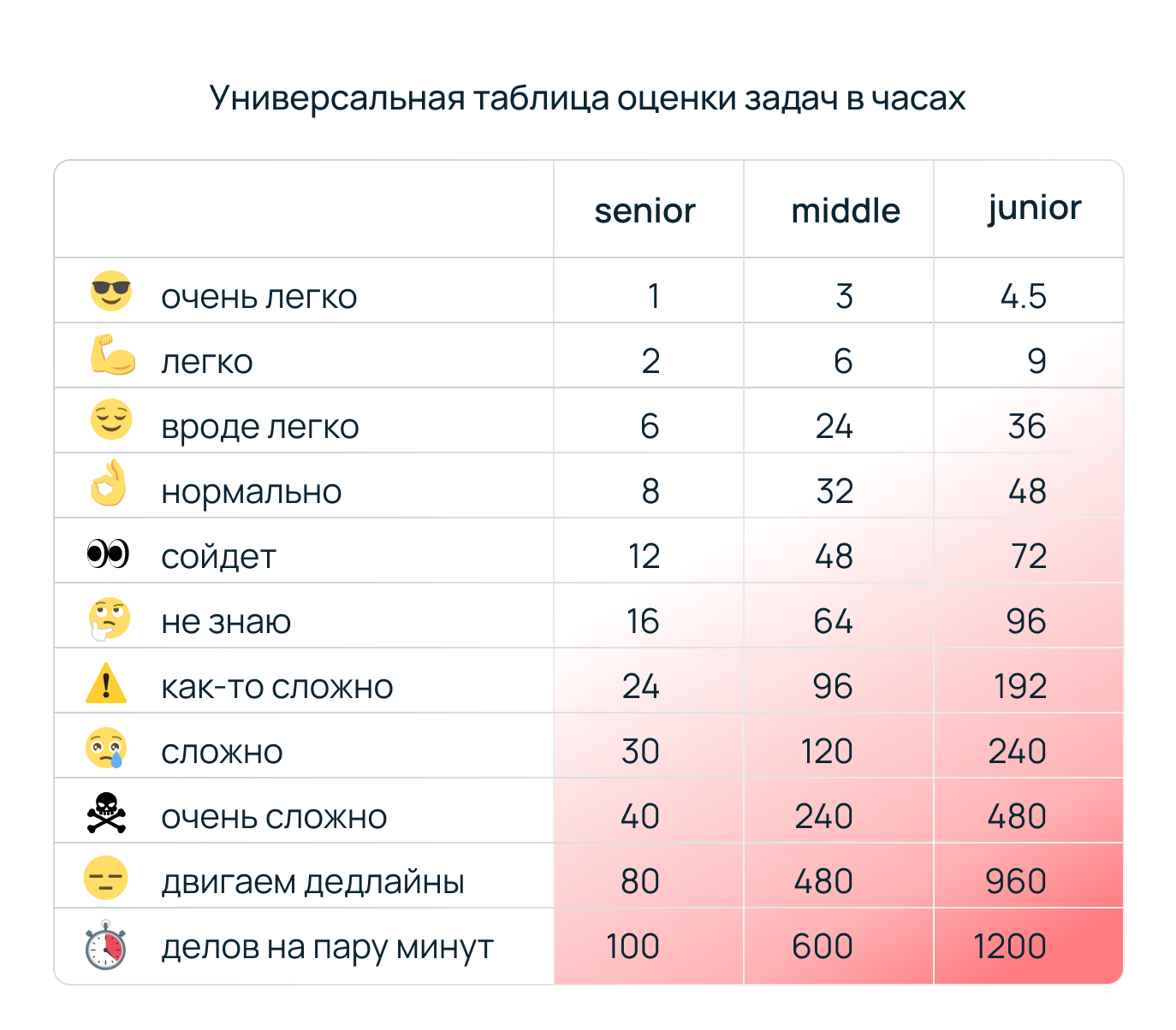
В этом тексте хочу исправиться: разбить знания по Data Science и машинному обучению на несколько теоретических блоков и дать больше полезных материалов.

Введение в проблематику

О численной оптимизации и других сложных темах

Хотелось бы отдельно поговорить о необходимости разговора о методах численной оптимизации. В статье про Data Science. Для начинающих.

Мне кажется, что на первых порах это слишком сложный раздел математики. Ведь чтобы научиться бегать, необходимо сначала научиться ходить, а перед этим — ползать. Но именно это замечание натолкнуло меня на мысль, что задача написать статью о том, как основательно подойти к своему профессиональному развитию в Data Science, далеко не так проста, как изначально казалось. На пути специалиста слишком много локальных экстремумов, а ландшафт ошибки, по которому приходится бродить, слишком ухабист.

При этом нет худа без добра. Я нашел для себя довольно любопытный курс по численным методам для инженеров от профессора университета Гонконга. Во втором видео говорится об ошибке округления, по поводу которой в комментариях дали хорошую ссылку. Уже в третьем видео автор курса рассказывает о стандарте IEEE, как в нем представлены числа, какие из них резервируются и т.д. А дальше уже есть видео и про методы Рунге-Кутта (ссылка, ссылка, ссылка).

Безусловно, понимание численных методов важно, если хочется знать, что происходит под капотом. Можно, например, вооружиться вот такой книжкой и уйти в тибетский монастырь на пару лет, чтобы от корки до корки ее прочесть. Можно попробовать пройти вот такой курс. 

Все это, тем не менее, лежит далеко за пределами уровня новичка. Поэтому я не включаю численную оптимизацию в свои подборки. Хочется-то другого. Хочется ровно того, о чем пишет в своей книге (о ней будет ниже) Михаил Юрьевич Пантаев:

«… адресат… — человек, отчасти напуганный математикой (а таково большинство студентов технических вузов средней руки), которому я бы хотел протянуть… гм… руку помощи. Нежную, понимающую руку».

Вот чего хочется. Помощи. Простой и человеческой. Я не тот, кто может ее оказать, но это могут сделать те, чьи книги, статьи и другие материалы будут подсвечены в этой статье.

У нас мало времени, нам не изучить все дисциплины!

Времени всегда мало, оно вечно куда-то ускользает. Между тем, сколько бы я ни пытался уложить различные разделы математики в единую картину, я нахожусь примерно там же, где был несколько лет назад.

Сбор материалов и работа над статьей помогли понять, что систематизация математики — это далеко не только моя проблема. Сравнительно недавно я наткнулся на доказательства данной мысли. Вот, например, что пишет или пишут (если вы понимаете, о чем я) Никола Бурбаки в своей статье «Архитектура математики»:

«…оказывается, что каждый год математическая наука обогащается массой новых результатов, приобретает все более разнообразное содержание и постоянно дает ответвления в виде теорий, которые беспрестанно видоизменяются, перестраиваются, сопоставляются и комбинируются друг с другом. Ни один математик не в состоянии проследить это развитие во всех подробностях, даже если он посвятит этому всю свою деятельность.

Многие из математиков устраиваются в каком-либо закоулке математической науки, откуда они и не стремятся выйти, и не только почти полностью игнорируют все то, что не касается предмета их исследований, но не в силах даже понять язык и терминологию своих собратьев, специальность которых далека от них. Нет такого математика, даже среди обладающих самой обширной эрудицией, который бы не чувствовал себя чужеземцем в некоторых областях огромного математического мира; что же касается тех, кто подобно Пуанкаре или Гильберту оставляет печать своего гения почти во всех его областях, то они составляют даже среди наиболее великих редчайшее исключение».

Нет, не изучить. Но мы все равно будем пытаться!

Пусть мы и не можем изучить всю математику, это не означает, что нужно прекращать попытки, ибо как гласит предисловие Рихарда Куранта в книге «Что такое математика»:

«На протяжении двух с лишним тысячелетий обладание некоторыми, не слишком поверхностными, знаниями в области математики являлось необходимой составной частью интеллектуального багажа каждого образованного человека».

Следовательно, если говорить об основательном подходе, то погружение в математику — это процесс, длиною, возможно, в целую жизнь. Станете ли вы при этом Head of Data Science department, получите ли ярлычок Competition Grand Master на Kaggle, возглавите ли кафедру по машинному обучению в своем университете — так ли это важно для вас?

Важнее ли для вас добиться какого-то выдающегося результата в этом деле или же радоваться тому, что находитесь на пути своего развития? Я не знаю, вам виднее. Для себя я более-менее все решил — поэтому «ковыряюсь» в книгах и пишу об этом.

Какой бы соблазнительной ни была идея остаться сугубо в процессе изучения математики, нужно признать: любой процесс с чего-то начинается. В нашем случае стоит начать с того, что позволяет нам обоснованно и непротиворечиво рассуждать. С чего именно — догадайтесь по фото:

Мужчина на фотографии довольно много говорил об этом в свое время. Конечно, он тогда еще не ходил с такой прической. Учитывая то, откуда эта фотография, он наверняка никогда не ходил с такой прической. Тем не менее, уж кто-кто, а он очень хорошо умел рассуждать. Догадались? Тогда можно идти дальше.

Вы — строитель, факты — ваши материалы, а логика — ваш молоток

На самом деле, не только логика. В один ряд с ней можно поставить риторику, теорию аргументации, когнитивистику, философию, историю и другое. Казалось бы, какое это отношение имеет к математике? Как говорил один математик устами своего безумного персонажа: «Что общего между вороном и письменным столом?»

Вопрос риторический. Тем не менее, позвольте мне привести контраргументы к тезису о слабой связи между темой статьи и перечнем гуманитарных дисциплин, которые я привел.

Наука о данных, машинное обучение, аналитика и обработка данных, построение моделей, их развертывание и последующий анализ — все это тесно связано с процессом построения рассуждений.

Каждый раз, когда мы решаем задачи, мы либо строим новую цепочку рассуждений, либо продолжаем строить ранее начатую. В этом процессе мы тот самый строитель. В роли строительных материалов выступают факты. Но что же будет в данной аналогии инструментом?

Логика

Вы можете быть отличным техническим специалистом, но если вы не можете четко и внятно рассказывать о том, что, как и зачем вы делаете, вам будет трудно общаться с коллегами и потенциальными работодателями.

Способность воспринимать поступающую информацию, критически ее осмыслять и выделять ключевое — важные навыки, которые можно в себе воспитать через изучение логики, риторики, аргументации и критического мышления. Это те навыки, которые позволяют вам осваивать новые технологии, адаптироваться, абстрагироваться от мелких деталей или же, наоборот, погружаться в них.

Воспитал ли я их в себе? О нет, отнюдь. Стараюсь ли? Определенно. Нужно ли вам этим заниматься? Вам решать. Я, пожалуй, просто оставлю несколько ссылочек ниже и дам выбор, прислушиваться ли к моим аргументам или нет.

Курс на Stepic: Логика

Крутой курс с большим количеством дополнительной литературы. После него фраза «Давайте определимся с понятиями» стала для меня более четкой и осмысленной.

Для повествования курс использует элементы теории множеств. На простом языке, без формализма и академической сухости, автор рассказывает о дедукции и индукции, отношениях между понятиями, суждениях и умозаключениях.

Источник → изучайте по ссылке.

Книга: Введение в логику для философов

Авторы этой книги ставят перед собой довольно сложную задачу — объяснить логику студенту-философу. Здесь сразу на ум приходит вопрос: что сложнее, рассказать кому-то правила игры или совместно эту игру переизобрести? На первый взгляд кажется, что первый вариант проще. Но что, если игра слишком сложна и ее правила писали несколько тысяч лет?

В самом начале книги говорится о том, что мы оперируем не реальными объектами, а их символьными двойниками. То есть рассуждая, мы пользуемся не объектами, а нашими представлениями о них, а символы — это ярлычки для наших представлений. Конечно, в таком случае было бы неплохо быть уверенным, что представления эти адекватны в реальности.

Стало быть, мы не можем оперировать символами, как нам вздумается. Точнее оперировать-то мы можем как угодно, но вопрос: с какой целью? Просто пофантазировать? Построить адекватное представление о мире? Выбить кого-то из равновесия? Если нас интересует второе, то некоторые вещи придется усвоить. Например, в чем разница между логиком и софистом, и уж тем более демагогом.

Вообще, в книге уделяется довольно много внимания теме знаков. Однозначно рекомендую к прочтению.

Книга: Как же называется эта книга

На моем курсе по математической логике был преподаватель. Он всегда носил один и тот же вязаный свитер зеленого цвета, а во время чтения лекции делал одинаковое количество проходок от одного края доски до другого. Откашливаясь, начинал новую тему. Однажды он, казалось, не мог вспомнить название книги, которую хотел порекомендовать. Только потом я понял, что все это — своеобразный троллинг.

Интересно, о чем эта книга? Хотите проверить свое мышление на прочность, разобраться в логике и просто повеселиться? Тогда советую почитать на досуге.

Источник → книга доступна по ссылке.

Риторика, теория аргументации и критическое мышление

Итак, вы пропитались законами логики, перестроили свое мышление под новый трафарет. Вы отделяете термины от понятий, пользуетесь принципом достаточного основания, иногда ловите себя на вопросе, доказано ли то, на что вы смотрите, или нет.

Этого достаточно? Честно, не знаю. 😅 Скажу другое: логика изучает корректность форм мышления, а вот содержание и, что еще важнее, цели мышления остаются за бортом. Между тем, содержание и цель мысли, очевидно, очень важны. Вопрос: как их распознать? На мой взгляд, ответ на этот вопрос будет проще найти, пройдя перечисленные ниже курсы.

Курс на Stepic: Риторика

Насколько хорошо вы доносите свои мысли до людей? Насколько четко способны их формулировать? Удавалось ли вам убеждать оппонентов в дискуссии? Как строится ваша речь? На все эти вопросы нельзя ответить однозначно, если вы не разбираетесь в риторике. Для первичного ознакомления с ней могу посоветовать курс от БФУ им. И. Канта.

Источник → изучайте по ссылке.

Курс на Stepic: Теория аргументации

Как часто бывает: смотрите видеоролик и не можете понять, с какой целью автор сказал то, что вы услышали? Какой риторический прием был только что использован? Заметили ли вы подмену понятия, или это была подмена тезиса?

Ответы на перечисленные выше вопросы можно найти в курсе о теории аргументации. Осторожно: после прохождения курса вы ахнете от того, как часто, небрежно и незамысловато вместо аргументов используются тезисы, нарушаются базовые законы логики, все мыслимые и немыслимые правила дискуссии.

Источник → изучайте по ссылке.

Курс на Stepic: Критическое мышление

Теперь вопрос: как же сделать так, чтобы перечисленные выше вопросы возникали регулярно? Как воспитать в себе привычку верифицировать поступающую информацию, соотносить ее с разными источниками, разделять на блоки и выстраивать в логическую последовательность? Как избавиться от привычки бездумно ретранслировать чужие мнения и убеждения?

Ответ: необходимо воспитывать в себе критическое мышление. Это не новое веяние, основы критического мышления уходят корнями в Древнюю Грецию. Вполне достаточно будет пробежаться по свежему отчету всемирного экономического форума, чтобы понять, как важны когнитивные навыки сегодня и насколько будут востребованы завтра.

Есть масса источников, которые можно использовать для погружения в тему критического мышления. Однако для того, чтобы первично «сориентироваться в вопросе», рекомендую пройти курс от ТГУ.

Источник → пройти курс можно по ссылке.

Один — это я, два — это теленок, три — это корова, 123! — это 1.21463e+205

Что произойдет, если брать какие-нибудь предметы из разных корзинок и сочетать их друг с другом? Точнее, сколько существует способов сочетать разные предметы?

Сколько существует способов сочетать по два предмета, по три, по 123? Если у меня есть корзинка с игрушками и я хочу понять, сколько есть способов вытащить оттуда N игрушек, какую формулу нужно применить? А что, если мне важно, в каком порядке эти игрушки вытаскивать?

Перечислительная комбинаторика

Примеры оторваны от жизни, согласен. Но тут можно вспомнить знаменитую притчу про шахматы, задачу про ход коня, задачу коммивояжера и еще много другого. Смысл понятен: в каждом примере нужно чего-нибудь посчитать.

Если посмотреть задачи на классическое определение вероятности, окажется, что без специфических формул не обойтись. Собственно, тут и появляется необходимость, чтобы эти формулы изучить, понять и научиться ими пользоваться. Речь, конечно же, о комбинаторике (она же перечислительная комбинаторика).

Перейдем к источникам.

Курс на Openedu: Основы комбинаторики

Данный курс я проходил на платформе Coursera, но с недавних пор он там исчез (как и многие другие курсы). Причины такого загадочного исчезновения установить не могу. Вообще никак.

Этот курс был одним из первых, которые я проходил. Больше всего понравился лектор. Андрей Михайлович хорошо и подробно объясняет материал, приводит много примеров, да и в целом его очень интересно было слушать. Понравится ли он вам, можете узнать, пройдя данный курс. Для того, чтобы «освоиться» в мире комбинаций, он отлично подойдет.

Источник → изучайте по ссылке.

Книга: Популярная комбинаторика

Об этой книжке я узнал во время написания статьи. Любопытно было почитать про Пьера Безухова, который пытается вывести число 666 из имени Наполеона Бонапарта. Вот интересно, а сейчас кто-нибудь пытается из чьего-нибудь имени это число вывести? Не знаю даже.

Бывает интересно находить свидетельства о том, как отдельные формулы, а порой и целые разделы современной науки берут свое начало из явно ненаучных течений. Для пифагорейцев числа носили мистический смысл, комбинаторными изысканиями занимались каббалисты и астрологи, а знания циркулировали от монастыря к монастырю — на эту тему рекомендую почитать роман Умберто Эко «Имя Розы».

Комбинаторика, как и любой другой раздел математики, обладает своей историей, взлетами и падениями, неожиданными поворотами. Погружение в данный контекст, понимание причин возникновения задач и методов решений, несомненно поможет лучше понять, как эти решения работают. Для такого погружения подойдет данная книга.

Источник → читайте по ссылке.

Книга: Комбинаторика

Эта книга не дает подробного исторического экскурса, но в понятной форме рассказывает о вопросах, связанных с комбинаторикой. Например, о правилах суммы и произведения, размещениях, перестановках, сочетаниях и другом. Все эти идеи проиллюстрированы на большом количестве задач и плавно выводятся друг из друга.

По каждой главе есть масса задачек на самоконтроль, так что скучать не придется. Я бы сказал, что одной этой книжки хватит, чтобы бодро погрузиться в область комбинаторики.

Источник → изучайте по ссылке.

Весь мир — множество, а люди в нем — элементы

Уже при изучении формальной логики вы почти сразу поймете, что ряд положений в ней объясняется через понятия, которые сводятся к множествам. Вот пример:

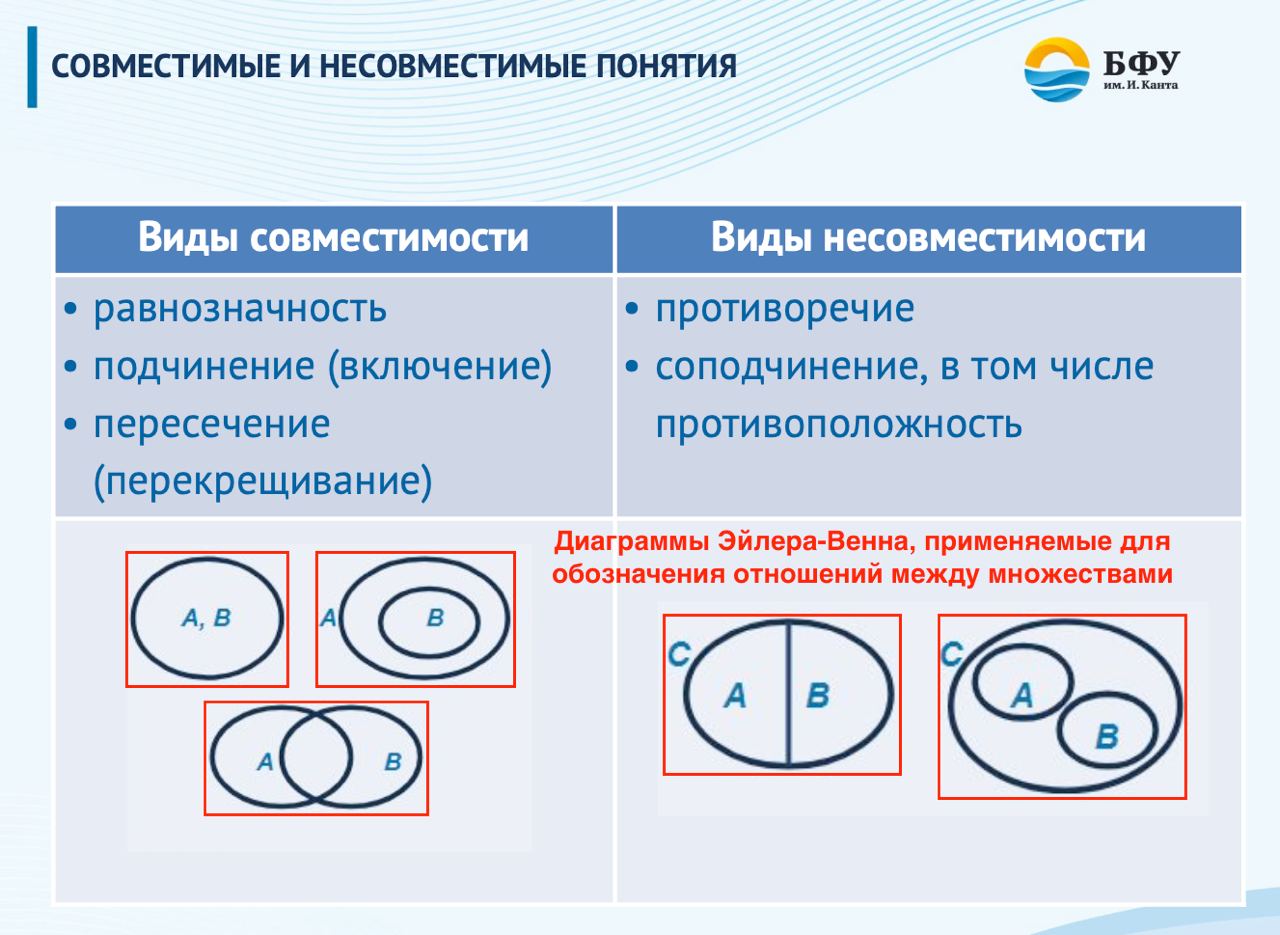
И это только из одной презентации по курсу логики. Между тем, понятия о множествах применяются далеко не только в логике.

Тут может возникнуть вопрос: зачем все это изучать? Какой смысл в том, чтобы штудировать часами определения и запутанные математические формулировки? А все довольно просто: математический анализ, линейная алгебра, теория вероятностей, математическая статистика, аппарат машинного обучения как дисциплины насквозь пронизаны понятиями из логики, теории множеств и общей алгебры.

Наверное, без всего этого можно обойтись. Можно зайти с практической стороны вопроса и погрузиться в PyTorch, Scikit-learn. Проблема такого подхода в том, что довольно скоро может появиться чувство, что вы не понимаете, что вообще происходит.

Почему код написан именно так, как написан? Как именно работает fit/predict? Зачем эти методы работают так, как работают? Для ответа на эти вопросы нужно хотя бы немного погрузиться в фундаментальные разделы математики, разобраться с базовыми определениями вроде многообразий, собственных векторов, изоморфизмов, градиентов и другого. Я попробовал собрать самое основное (с точки зрения теории множеств и общей алгебры), в чем нужно разобраться:

На схеме стрелочками я обозначил приблизительную последовательность погружения в понятия и определения, которые встречаются в упомянутых дисциплинах. Конечно, это достаточно грубый набросок, ведь в реальности все будет несколько сложнее. Тем не менее, если кому-то эта схема сэкономит время, это можно считать успехом.

Теперь давайте вернемся к полезным источникам и посмотрим, что можно изучить для погружения в теорию множеств, которую принято разделять на наивную и аксиоматическую.

Наивная теория множеств

Курс на Coursera: Data Science Math Skills

Скажу честно: курс я полностью не проходил. Но успел просмотреть основные темы и порешать задачки. Они довольно простые и хорошо подойдут, если вы только начинаете свой путь в теории множеств. Лекторы с заботой рассказывают о тех понятиях и обозначениях, с которыми вы встретитесь впоследствии.

Источник → изучайте по ссылке.

Книга: Дискретная математика. Теория и практика

Во время аспирантуры я провел много бессонных ночей, пытаясь разобраться в сложной цепочке понятий, которая описана в этом пособии. Рекомендую его к ознакомлению, потому что в нем отлично изложен материал по теории множеств, который плавно переходит к общей алгебре.

В книге есть довольно много примеров, по которым можно лучше понять, как работают понятия и определения выше. Отдельно могу выделить действительно полезный список литературы, пригодится каждому математику.

Источник → читайте книгу по ссылке.

Книга: Начала теории множеств

Если предыдущая книга довольно сжато излагает теорию множеств, то данное пособие дает больше интуитивно понятного описания и иллюстраций.

Источник → читайте книгу по ссылке.

Аксиоматическая теория множеств

Бреет ли себя брадобрей, если он бреет тех и только тех, кто сам себя не бреет? Хвалит ли себя артист, если он хвалит только тех, кто сам себя не хвалит? Бурбулит ли себя бурбуль, если он бурбулит только тех бурбулей, которые сами себя не бурбулят? Все это — парадокс брадобрея (Бурали-Форти).

На тему этого парадокса есть довольно интересное пособие от московского центра непрерывного математического образования, которое рассказывает о нестыковках наивной теории множеств. Парадокс Бурали-Форти иллюстрирует ситуацию, когда множество определяется так, что возникают элементы, которые в него одновременно входят и не входят.

Можно ли в принципе обнаружить летающего крокодила, который бы никогда не побеждал во всероссийской олимпиаде по математике? Очевидно, что нет. Получается, все летающие крокодилы являются победителями всероссийской олимпиады по математике.

В данном варианте, конечно, особо никакого парадокса нет: просто фраза «летающие крокодилы» описывает пустое множество. Однако он, как и предыдущий пример, показывает, что произвольно заданное множество может приводить к ситуациям, над которыми придется долго ломать голову.

Чтобы свести такие парадоксы к минимуму, ученые Цермело и Френкель ввели «несколько» правил, которые назвали аксиомами и вывели в аксиоматическую теорию множество.

Книга: Парадоксы теории множеств

Рекомендую прочитать это пособие всем. Авторы на понятном языке описывают проблемы, в результате которых аксиоматическая теория множеств вообще появилась.

Возможно, нет смысла разбирать все примеры и читать пособие от корки до корки. Однако для того, чтобы прокачать знания в теории множеств, этого пособия будет достаточно. Лично мне понравилось доказательство отсутствия равномощности множества с множеством его подмножеств.

Источник → изучайте по ссылке.

Книга: Рассказы о множествах

Сложно сказать, как часто попадаются книги по математике, где было бы живое изложение материала. Пожалуй, эта книга одна из таких. Автор предлагает свой вариант «коридорной» подготовки по теории множеств, приводит разнообразные примеры по типу великой переписи рыб или гостиницы, где бесконечно много номеров.

Из книги, правда, я не очень понял, как именно строятся трансфинитные числа, но на эту тему лучше почитать отдельное пособие.

Источник → изучайте по ссылке.

Видео на YouTube: Теория множеств: логика, формализм и кризис

Это видео — толковый экскурс в историю появления аксиоматики теории множеств. Оно дает много пищи для рассуждений о том, насколько иллюзорной является стройность и непротиворечивость математики как явления.

Логически видео поделено на несколько глав. Первая рассказывает о том, как формировалась наивная теория множеств, как она пропитала собой всю математику и стала ее фундаментом.

Вторая глава рассказывает о первых парадоксах в наивной теории множеств. Третья — посвящена фундаментальным принципам формирования математики: логицизму, интуиционизму, формализму и теоретико-множественному подходу. Отсюда начинаются разговоры про непротиворечивость, про аксиоматику Цермело-Френкеля. Четвертая глава рассказывает, что помимо непротиворечивости есть еще и полнота. Наконец, пятая — подводит итоги, упоминает теорию категорий в современной математике.

Источник → изучайте по ссылке.

Объекты не столь существенны, важны их отношения

Есть такой замечательный учебник по теории вероятностей за авторством Натальи Черновой. Если вы откроете его оглавление, то уже в третьей главе увидите параграф «Алгебра и сигма-алгебра событий». Соответствующее видео по этой теме можно посмотреть по ссылке.

Один из разделов — «Борелевская σ-алгебра в ℝ». Третья глава как бы намекает, что без крепкого понимания алгебры, счетной аддитивности, понимания меры Лебега и нормированной меры невозможно понять определение вероятности, которое вводится дальше.

Возможно, я драматизирую. В конце концов, вы, читатели, хотите изучить Data Science, а не обуздать математику с тысячами формул, определений и доказательств. Может, достаточно просто прочитать учебник по работе с данными? Такая точка зрения имеет право на жизнь — давайте так и попробуем сделать.

Откроем, например, учебник по машинному обучению, составленный — цитирую — «коллективом добрых людей из преподавателей и выпускников Школы анализа данных». В начале книги нас встречает такое предисловие:

Похоже, ничего страшного нет, можно идти дальше. Но в разделе 2.1 про метод наименьших квадратов нас встречает следующее:

Короче, если люди говорят о необходимости во владении линейной алгеброй, будьте готовы к тому, что они ровно это и имеют в виду. Это будет не просто большим, а решающим плюсом.

Похоже без линейной алгебры не обойтись. Но постойте:

А может быть все иначе с математическим анализом? Может, все эти поля с кольцами и группами особо и не нужны?

Ну, можно попробовать глянуть, например, первый том Владимира Антоновича Зорича по математическому анализу (глава вторая, параграф первый):

Обратите внимание на «странные» символы рядом с цифрами — это аксиомы сложения:

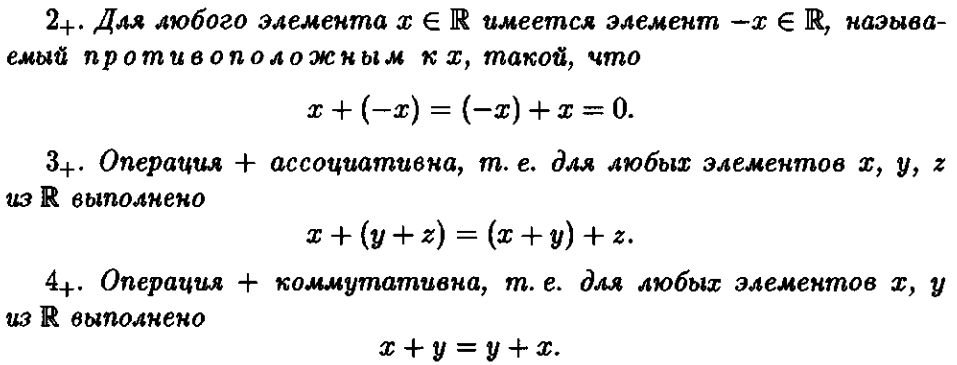
Это ведь были только аксиомы по операции сложения, а ведь у нас еще и умножение есть:

И вы представляете:

Да, выясняется, что и тут понятия, введенные в общей алгебре, прочно вплетаются во все построения, на базе которых весь аппарат математического анализа и работает.

Общая алгебра

Давайте вернемся к источникам и посмотрим, что можно почитать, чтобы оперировать математическими понятиями и уметь их воспринимать правильно. Надеюсь, к этому моменту мне удалось вас убедить, что изучение общей алгебры может быть полезно для погружения в науку о данных.

Здесь, правда, как и с теорией множеств, возникает проблема: общая алгебра не сильно популярна на просторах Stepic и Coursera. Поэтому могу порекомендовать только отдельные видео и учебники.

Видео на YouTube: Общая алгебра. Основные понятия и математическая красота

Это видео — хороший способ зародить интерес к общей алгебре. Автор рассказывает о том, что такое структуры типа группы, кольца и поля. А также затрагивает тему гомоморфизма и изоморфизма алгебраических структур. Кроме того, в самом описании к видео есть несколько материалов, на которые можно обратить внимание.

На канале этого автора есть подборка видео по истории математики, откуда можно почерпнуть много интересного о том, как зарождалась общая алгебра.

Источник → изучайте по ссылке.

Книга: Лекции по общей алгебре

Это уже действительно большой труд, читать который целиком, по моему мнению, смысла нет, но пару глав разобрать стоит. В первой автор разбирает основные понятия, которые уже вводились в пособии по дискретной математике. Среди них — отображения, отношения, их свойства и другое.

Вторая глава начинает вводить различные алгебраические структуры типа группоида, полугруппы, группы, кольца, тела, поля и другого. Текст изложен в строгом стиле, но понятия вводятся последовательно. Впрочем, если стиль изложения покажется чересчур формалистичным, можно также почитать введение в абстрактную алгебру венгерского математика Эрвина Фрида.

Я бы сказал, для более осознанного изучения целевых дисциплин стоит брать материал выборочно: взять первые две главы для ознакомления, а последующие читать сугубо при возникновении с книгой «глубокого взаимного чувства».

Источник → изучайте по ссылке.

Видео на YouTube: Цикл лекций Николая Вавилова по высшей алгебре

Сложно переоценить объем данного курса. Также тяжело сказать, до какой степени нужно в него погружаться.

Сам я полностью этот курс не проходил, хотя желание было. Имеет смысл поставить лекции на x1.5 и слушать по мере возможности (я так и делал). Посмотрите сами, за что зацепится ваш слух, и изучайте эту тему более тщательно.

Источник → изучайте по ссылке.

Видео на YouTube: Элементарное введение в теорию групп

Очень наглядные короткие видео, с помощью которых можно погрузиться в теорию групп. Автор дает небольшую предысторию возникновения этой дисциплины, приводит несколько примеров, на которых наглядно демонстрируются понятия (операции, замкнутости и другое).

Операции формально могут быть определены так, что для них будут работать одни свойства, а другие — не будут. Или будут существовать или не существовать симметричные или нейтральные элементы соответственно. Они могут быть определены частично, быть замкнутыми или незамкнутыми относительно того множества, на котором эти операции проводятся.

В сухом остатке каждая такая уникальная комбинация множества, определенных на нем операций, их свойств, наличия или отсутствия симметричных и нейтральных элементов, порождает уникальную алгебру, которая может быть как изучена, так и применима в реальном мире.

Источник → изучайте по ссылке.

Линейная алгебра

Я уже говорил, что линейная алгебра — особенно важный раздел математики, если говорить именно о Data Science и машинном обучении. Для примера: все операции с нейросетями — матричные.

Проблема в том, что сама по себе линейная алгебра имеет высокий порог вхождения. По крайней мере, мне так показалось, когда я начинал. Формулы выдавались как рецепты, их смысл объяснять никто особо не удосужился. Надеюсь, источники ниже помогут залатать эти пробелы.

Видео на YouTube: Сущность линейной алгебры

Пересмотрел серию этих видео несколько раз — думаю составить по ним конспект. Больше всего мне понравилось, насколько наглядно авторы излагают материал. Есть даже полноценная библиотека, с помощью которой можно визуализировать данные в стилистике видео 3Blue1Brown.

Видео однозначно рекомендую к ознакомлению. Автор очень хорошо понимает то, о чем говорит.

Источник → смотрите видео по ссылке.

Видео на YouTube: The Bright Side of Mathematics — Linear Algebra

После видео 3Blue1Brown рекомендую посмотреть серию видео от The Bright Side of Mathematics. На мой взгляд, видео данной серии менее наглядны, но покрывают больше тем. Автор довольно детально рассматривает каждый вопрос. За данную ссылку спасибо доброму человеку, который упомянул The Bright Side of Mathematics в комментариях к первой статье.

Источник → изучайте по ссылке.

Книга: Линейная алгебра и некоторые ее приложения

Отличная книга по линейной алгебре. Спасибо проекту LAPLAS, которые рассказали про нее в одном из своих видео.

Мне понравилось, как автор объяснила смысл определителя в самом начале. Если в серии роликов есть наглядная геометрическая интерпретация определителя, то в данной книге — не менее понятное объяснение на базе систем уравнений.

Вторая глава уже требует понимания идеи алгебраической структуры — в частности, поля. Конечно, книга довольно гладко вводит его определение, что ее только красит. В следующих главах идет обсуждение линейной зависимости, комбинации, базиса, размерности и других тем.

Когда-то мне было сложно понять, зачем вообще эти определения понадобились, к чему вся эта эквилибристика с «буковками». Первая серия видео поможет построить интуитивное понимание через наглядные визуализации, а вторая, в паре с этой книгой, — поможет его зафиксировать.

Источник → изучайте по ссылке.

Бесконечность — не предел, не мера и не норма

Однако каждый математик должен их знать, если верить одной крылатой фразе, авторство которой я так и не смог установить. А вообще, бойтесь крылатых фраз, какими бы красивыми ни были крылья!

Это я к тому, что во всем упомянутом разнообразии математики есть раздел, который вы встретите в теории вероятностей, математической статистике и других дисциплинах. Речь о математическом анализе.

Мало кто удивится тому, что метод обратного распространения ошибки является применением правила дифференцирования сложной функции. Тем не менее, есть даже целое расследование на тему того, кто же все-таки изобрел данный метод. Это довольно яркое свидетельство того, что все новое — давно забытое старое.

Математический анализ

Без математического анализа, на мой взгляд, заниматься той же теорией вероятностей будет сложновато. Связь между функциями и плотностями распределения вероятности, определение начальных и центральных моментов, предельная теорема скрывают в себе интегралы, производные и пределы.

Как вам частные производные? Что будет, если взять и выставить их в ряд и пронумеровать? Знаете, что получится? Да, будет градиент. Тот самый, который применяется при градиентном спуске, который применяется в глубоком обучении, которое применяется в… — думаю, вы поняли. Возвращаемся к полезным источникам.

Видео на YouTube: Суть матанализа

После просмотра части этих видео возникли примерно те же ощущения, как от плейлиста «Суть линейной алгебры». Все просто, понятно и очень наглядно. Без сухих доказательств и формул — только решения реальных задач.

Источник → изучайте по ссылке.

Книга: Семь семинаров по математическому анализу

До сих пор это самая необычная книжка по математическому анализу. Спасибо за нее сообществу «Партизанская математика». Книжка вроде и про «матан», а напоминает скорее художественный роман. Такой, в котором учитель беседует со своими учениками, задает им вопросы, корректирует и дополняет. А ты будто становишься частью этой беседы. Чем-то напомнило фильм «Агора».

Источник → изучайте по ссылке.

Книга: Матанализ с человеческим лицом, или как выжить после предельного перехода

Еще одна крутая и необычная книжка по математическому анализу. За нее также спасибо сообществу «Партизанская математика».

Первая глава подробно рассказывает о возникновении задач, где появляется необходимость работать с чем-то, похожим на интегрирование (метод исчерпывания), с чем-то, что так или иначе затрагивает бесконечность.

Вторая глава начинается с отличной цитаты: «История математики обладает одним неисправимым недостатком: хронологический порядок событий не соответствует порядку логическому, естественному». Верное замечание.

Эта глава в целом рассказывает о том, что отцам-основателем «матана» не чужды шалости в стиле «когда надо — h равно 0, а когда не надо — не равно». И что путь формирования того строгого аппарата, который поставлен на вооружение математического анализа, далеко не всегда был таким.

Автор обсуждает с читателем парадоксы, доказательства, а также тот факт, что — приготовьтесь — не все в этой жизни можно определить. Поэтому книга «Матанализ с человеческим лицом» далеко не только про «матан». Рекомендую к прочтению.

Источник → изучайте по ссылке.

Заключение

Вот и подошла к концу вторая статья по источникам. Спасибо, что уделили время на прочтение. Надеюсь, что вы его не потратили зря и смогли вынести что-нибудь полезное.

За скобками осталась теория вероятностей, методы численной оптимизации, математическая статистика и многое-многое другое, но это можно оставить на будущее.

Что я для себя понял за время написания статьи: непротиворечивая систематизация знаний в очередной раз мне не далась — и в этом нет ничего страшного. Потому что путь важнее назначения. И кто знает, может, вы станете одним из тех попутчиков, кто в комментариях поделится своим опытом, знанием и просто рекомендациями.

В очередной раз напомню: чтобы стать специалистом, нужно основательно подойти не только к теории, но и следить за новыми технологиями в мире машинного обучения и Data Science. Кстати, с последним мы помогаем в нашем Telegram-сообществе «MLечный путь». Там мы публикуем еженедельные дайджесты по DataOps и MLOps, обсуждаем проблемы и лучшие практики по организации production ML-сервисов, а также обмениваемся опытом. Присоединяйтесь к более 1800 специалистам, развивающим ML- и Data-направления в российских и зарубежных компаниях.