Задача о симметричной матрице

Условие

Студенту Алёше пообещали, что закроют долги только в том случае, если тот займет призовое место в олимпиаде по спортивному программированию. Они наверняка это сделали с издевкой, но нашему герою больше ничего не остается. В назначенный преподавателем день Алёша пришел на олимпиаду, уселся за парту, взял лист с бумагой, открыл первое задание и увидел матрицу.

«При чем здесь судоку?», — подумал герой и уже было испугался, но решил прочитать условие.

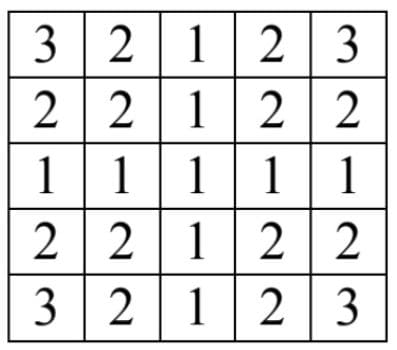
Из условия: нужно написать программу, которая заполнит массив размерности NxN (1 < N <= 100) по правилу на картинке. Кажется, что все довольно просто: сколько матрицу не транспонируй, «картина» не изменится. Да и формул здесь никаких знать не надо. Или надо? Алёша без проблем бы решил задачу, если бы не прогуливал пары.

Задача

Вы — друг Алексея, который пришел на олимпиаду за компанию. Помогите же решить герою задачу и построить симметричную матрицу — тогда он, возможно, не будет отчислен с курса и угостит вас шавермой. 

Как вы подойдете к решению задачи? Напишите код алгоритма на Python — Алёша ничего кроме него не знает.

Решение

Давайте крутить-вертеть матрицу — посмотрим, что изменится.

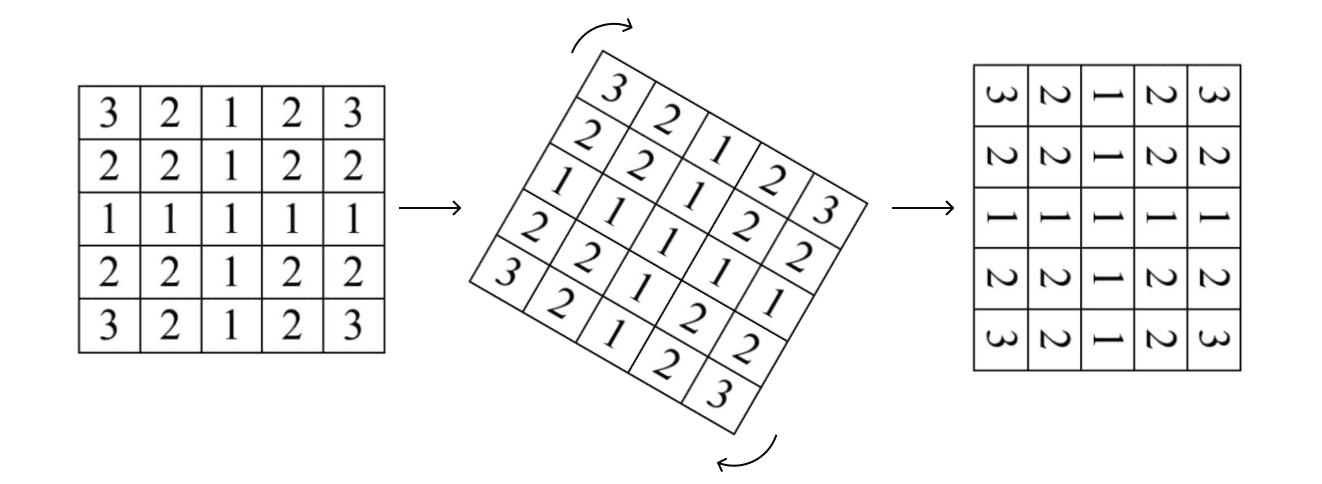
Ничего не изменилось. Это было очевидно: матрица симметрична относительно вертикали и горизонтали. А что будет, если ее пропорционально растянуть на один столбец и одну строку?

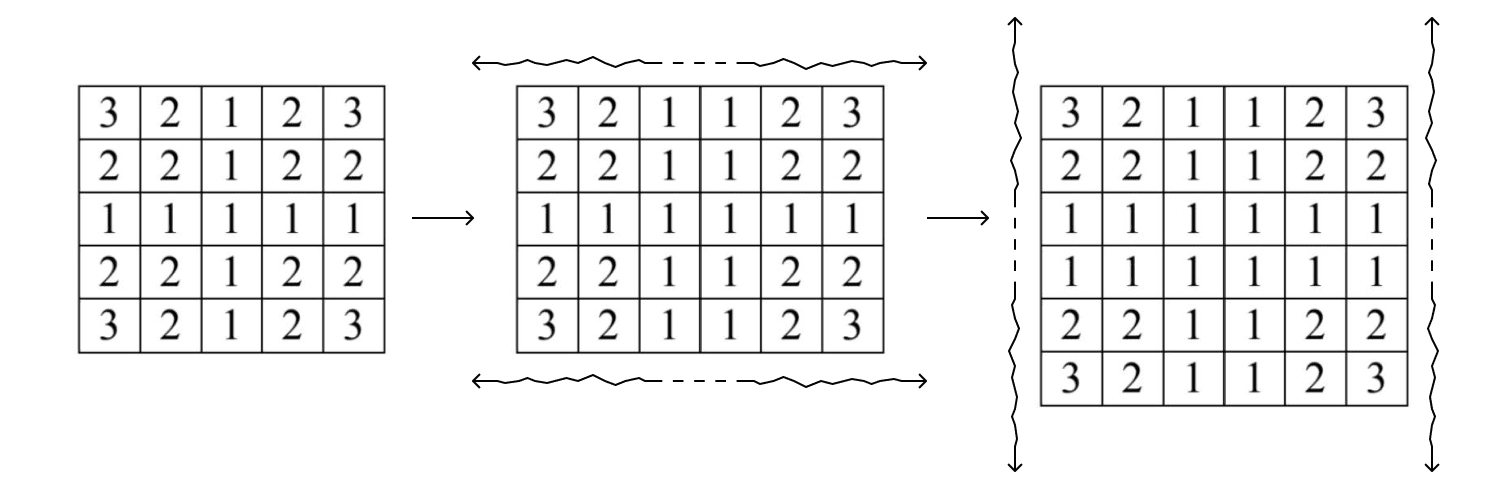
Получается, матрица может состоять из четного количества строк и столбцов! Это не указано в условии явно, но N может принимать любые значения от 2 до 100, что важно учесть.

Далее в глаза бросаются два пути. Например, можно вычислить значения для каждой ячейки матрицы по формулам, будто мы — настоящие математики. Кстати, таким образом легко определить, каким будет крайний элемент в матрице 7×7: 

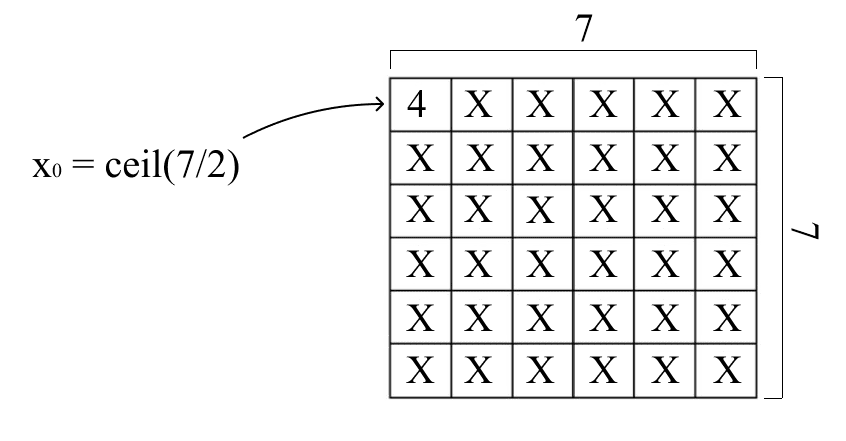
Формула нам пригодится, но расписывать ее для каждой ячейки не будем. Этот способ хоть и красивый, но слишком трудозатратный: Алёша не особо разбирается в математике, поэтому решение никогда не объяснит, если вдруг спросят.

Есть способ проще. Представим, что наша матрица — система координат, а горизонтальная и вертикальная оси — последовательности из целых чисел от -4 до 4. 

Тогда нам известны как минимум одна строка и один столбец:

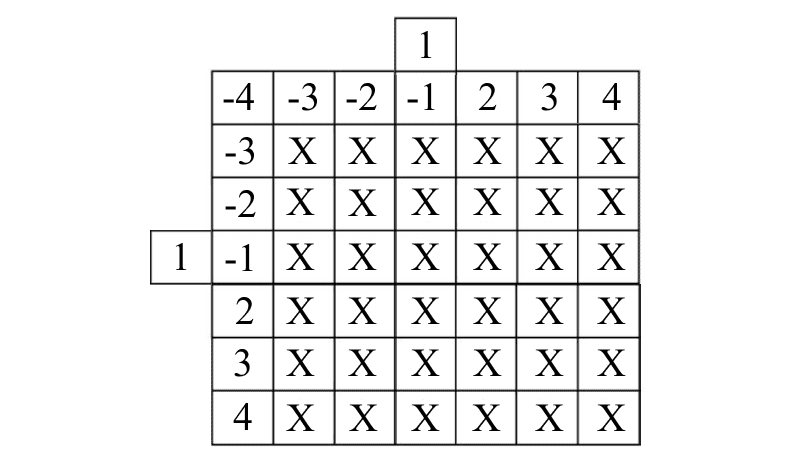
Наличие отрицательных чисел и пересечений хоть и бросается в глаза, но мало нас волнует. В Python достаточно использовать функцию abs, чтобы записывать значения без злополучного минуса, а на стыке двух 1 выбирать что-то одно:

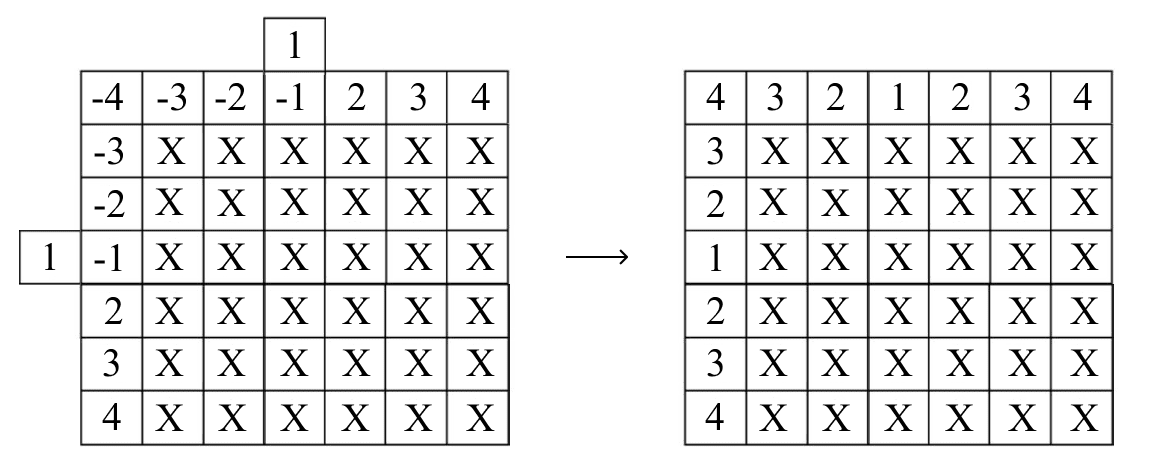
Дальше все гораздо проще. Получить X в любой из ячеек можно с помощью простой функции min. Как это работает? Посмотрите сами. Значение ячейки на пересечении 3 и 2 будет равно 2. Мы просто взяли минимальное значение координаты. При этом неважно, x это или y. Если x меньше y — в ячейку записываем x, а если y меньше — y. Это правило справедливо для всех ячеек матрицы — закодируем его:

    lower, upper = -(N // 2), (N // 2)

# проходим по элементам горизонтальной последовательности
for i in range(lower, upper+1):
    if N % 2 == 0 and i == 0: continue

    # проходим по элементам вертикальной последовательности
    for j in range(lower, upper+1):
        if N % 2 == 0 and j == 0: continue
        print(min(abs(j), abs(i)) + (N % 2), end=" ")
    print()

Готово — мы написали программу, которая позволяет генерировать полностью симметричные матрицы при четной и нечетной размерностях. Алёше наше решение нравится, ведь временная сложность алгоритма составляет O(N^2) — лучшего решения на олимпиаде никто не нашел.

Заключение

Хоть наш герой и вылетел на следующем этапе олимпиады и был отчислен из университета, он вам благодарен. Угостил после пар шавермой, а вы — подарили доступ к рассылке Академии Selectel, в которой собраны актуальные материалы про IT-технологии и не только. Если Алёша захочет подтянуть свои знания и навыки, она ему точно понадобится.