Ждет ли машинное обучение стагнация?

Сейчас потребности новых моделей машинного обучения (ML) растут гораздо быстрее, чем производительность компьютеров. И по этой причине многие задачи ML не будут решены никогда в силу физических ограничений вычислителя.

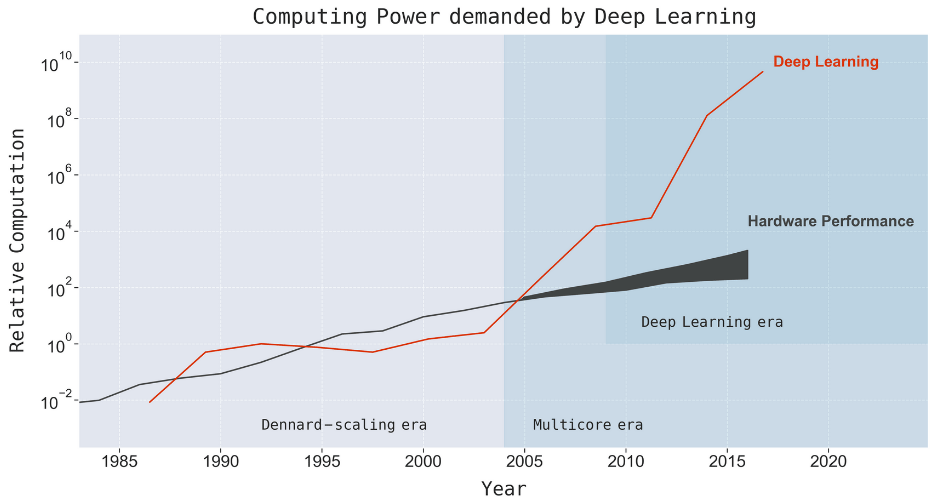
Последние годы глубокого обучения — сплошная череда достижений: от победы над людьми в игре Го до мирового лидерства в распознавании изображений, голоса, переводе текста и других задачах. Но этот прогресс сопровождается ненасытным ростом аппетита к вычислительной мощности.

Группа ученых из MIT, Университета Ёнсе (Корея) и Университета Бразилиа опубликовала метаанализ 1058 научных работ по машинному обучению. Он явно показывает, что прогресс в области машинного обучения (ML) — это производная от вычислительной мощности системы. Производительность компьютеров всегда ограничивала функциональность ML, но сейчас потребности новых моделей ML растут гораздо быстрее, чем производительность компьютеров.

Исследование демонстрирует, что достижения машинного обучения по сути — немногим более чем следствие закона Мура. И по этой причине многие задачи ML не будут решены никогда в силу физических ограничений вычислителя.

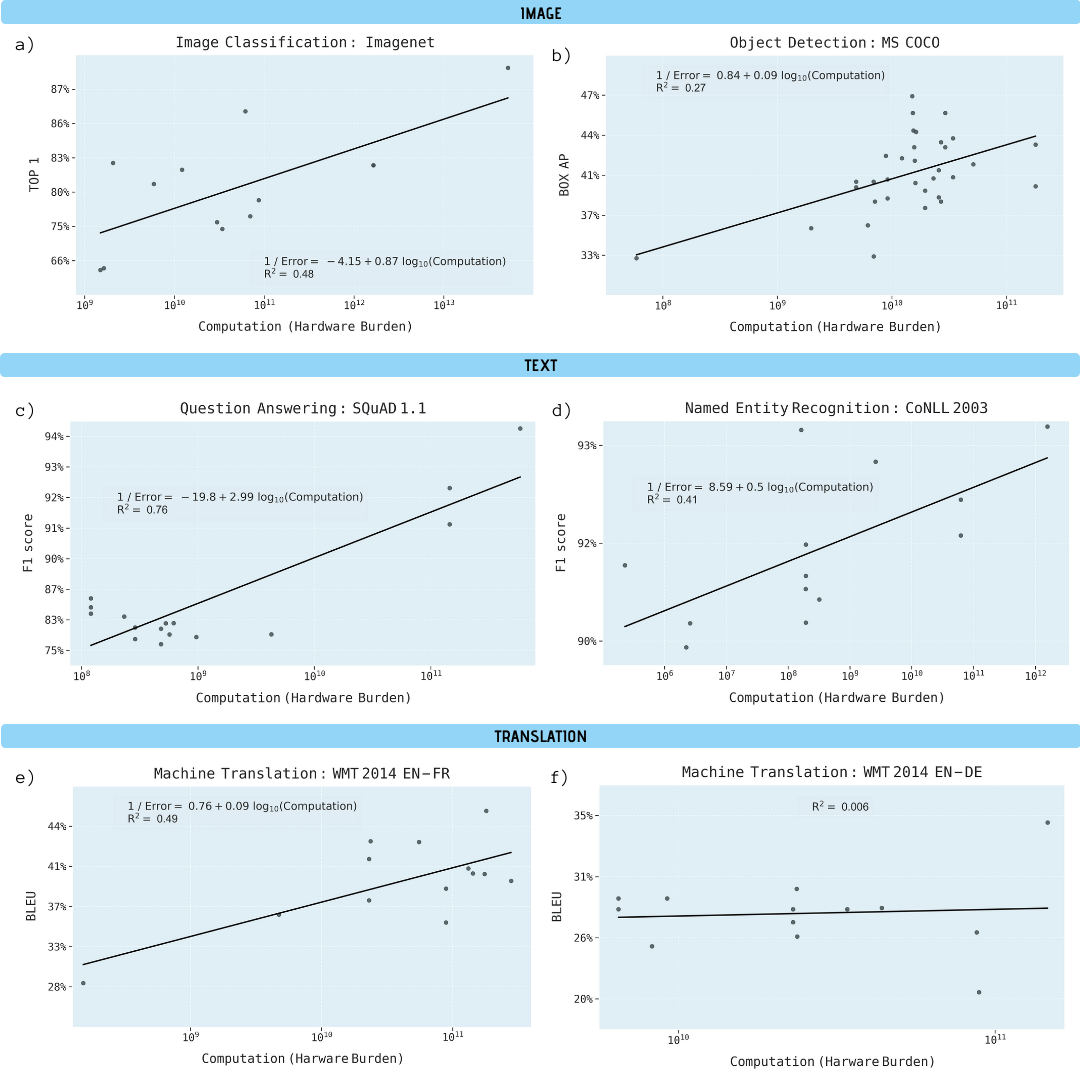
Исследователи проанализировали научные работы по классификации изображений (ImageNet), распознаванию объектов (MS COCO), ответам на вопросы (SQuAD 1.1), распознаванию именованных сущностей (COLLN 2003) и машинному переводу (WMT 2014 En-to-Fr).

Показано, что прогресс во всех пяти областях сильно зависит от увеличения вычислительной мощности. Экстраполяция этой зависимости дает понять, что прогресс по данным направлениям быстро становится экономически, технически и экологически неустойчивым. Таким образом, дальнейший прогресс в этих приложениях потребует значительно более эффективных с вычислительной точки зрения методов.

Почему машинное обучение настолько зависит от вычислительной мощности

Есть важные основания полагать, что глубокое обучение по своей природе более зависит от вычислительной мощности, чем другие методы. В частности, из-за роли гиперпараметризации и того, как масштабируется система, когда используются дополнительные обучающие данные для повышения качества результата (например, для уменьшения частоты ошибок классификации, среднеквадратичной ошибки регрессии и т.д.).

Было доказано, что значительные преимущества дает гиперпараметризация, то есть реализация нейронных сетей с количеством параметров больше, чем количество точек данных, доступных для ее обучения. Классически это привело бы к переобучению. Но методы стохастической градиентной оптимизации обеспечивают регуляризующий эффект за счет ранней остановки, переводя нейронные сети в режим интерполяции, где обучающие данные подходят почти точно, сохраняя при этом разумные прогнозы по промежуточным точкам. Пример крупномасштабных сетей с гиперпараметризацией — одна из лучших систем распознавания образов NoisyStudent, у которой 480 млн параметров на 1,2 млн точек данных ImageNet.

Проблема гиперпараметризации состоит в том, что число параметров глубокого обучения должно расти по мере роста числа точек данных. Поскольку стоимость обучения модели глубокого обучения масштабируется с произведением числа параметров на число точек данных, это означает, что вычислительные требования растут как минимум в квадрате числа точек данных в гиперпараметризованной системе. Квадратичное масштабирование еще недостаточно оценивает, как быстро должны расти сети глубокого обучения, поскольку объем обучающих данных должен масштабироваться гораздо быстрее, чем линейно, чтобы получить линейное улучшение производительности.

Рассмотрим генеративную модель, у которой 10 ненулевых значений из возможных 1000, и рассмотрим четыре модели для попытки обнаружить эти параметры:

• Модель с оракулом: у нее 10 точных параметров в модели
• Экспертная модель: 9 правильных и 1 неправильный параметр
• Гибкая модель: все 1000 потенциальных параметров в модели, и использует оценку методом наименьших квадратов
• Регуляризованная модель: как и гибкая модель, тоже задействует все 1000 потенциальных параметров, но теперь в регуляризованной модели (лассо)

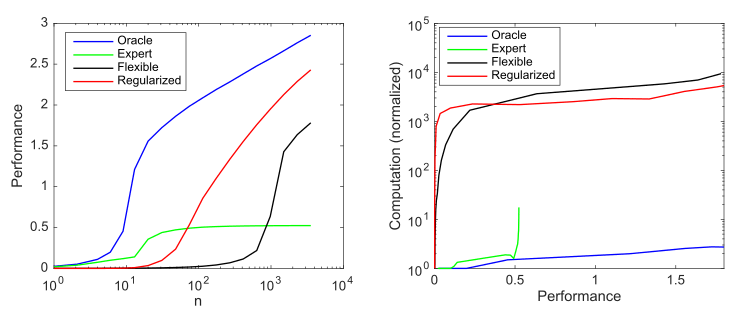
Этот график обобщает принцип, изложенный Эндрю Ыном: традиционные методы машинного обучения лучше работают на малых данных, но гибкие модели ML лучше работают с большими данными. Общий феномен гибких моделей заключается в том, что у них более высокий потенциал, но также значительно больший объем данных и вычислительные потребности.

Мы видим, что глубокое обучение работает хорошо, потому что использует гиперпараметризацию для создания очень гибкой модели и (неявную) регуляризацию, чтобы уменьшить сложность выборки до приемлемой. В то же время, однако, глубокое обучение требует значительно больше вычислений, чем более эффективные модели. Таким образом, увеличение гибкости ML подразумевает зависимость от больших объемов данных и вычислений.

Вычислительные пределы

Производительность компьютеров всегда ограничивала мощность систем ML.

Например, Фрэнк Розенблатт описал первую трехслойную нейросеть в 1960 году. Были надежды, что она «продемонстрирует возможности использования перцептрона в качестве устройства распознавания образов». Но Розенблатт обнаружил, что «по мере увеличения числа соединений в сети нагрузка на обычный цифровой компьютер вскоре становится чрезмерной». Позже в 1969 году Мински и Паперт объясняли ограничения трехслойных сетей, включая неспособность обучиться простой функции XOR. Но они отметили потенциальное решение: «Экспериментаторы обнаружили интересный способ обойти эту трудность путем введения более длинных цепочек промежуточных единиц» (то есть путем построения более глубоких нейронных сетей). Несмотря на этот потенциальный обходной путь, бóльшая часть академической работы в этой области была заброшена, потому что в то время просто не было достаточно вычислительной мощности.

В последующие десятилетия улучшения в аппаратном обеспечении обеспечили повышение производительности примерно в 50 000 раз, а нейронные сети пропорционально увеличили свои вычислительные потребности, как показано на КДПВ. Так как рост вычислительной мощности на один доллар примерно соответствовал вычислительной мощности на один чип, экономические затраты на запуск таких моделей оставались в значительной степени стабильными с течением времени.

Несмотря на такое значительное ускорение CPU, модели глубокого обучения еще в 2009 году оставались слишком медленными для крупномасштабных приложений. Это вынуждало исследователей сосредоточиться на моделях меньшего масштаба или использовать меньше примеров для обучения.

Поворотным моментом стал перенос глубокого обучения на GPU, что сразу дало ускорение в 5-15 раз, которое к 2012 году выросло до 35 раз и которое привело к важной победе AlexNet на конкурсе Imagenet 2012 года. Но распознавание изображений было лишь первым бенчмарком, где выиграли системы глубокого обучения. Вскоре они победили в обнаружении объектов, распознавании именованных сущностей, машинном переводе, ответе на вопросы и распознавании речи.

Внедрение глубокого обучения на GPU (а затем ASIC) привело к широкому распространению этих систем. Но объем вычислительной мощности в современных системах ML рос еще быстрее, примерно в 10 раз в год с 2012 по 2019 год. Эта скорость намного выше, чем общее улучшение от перехода к GPU, скромный прирост от последнего издыхания закона Мура или от повышения эффективности обучения нейронных сетей.

Вместо этого основной рост эффективности ML произошел от запуска моделей в течение большего времени на большем количестве машин. Например, в 2012 году AlexNet обучалась на двух GPU в течение 5-6 дней, в 2017 году ResNeXt-101 обучалась на восьми GPU в течение более 10 дней, а в 2019 году NoisyStudent обучалась примерно на тысяче TPU в течение 6 дней. Другим крайним примером является система машинного перевода Evolved Transformer, которая при обучении использовала более 2 млн часов GPU, что стоило миллионы долларов.

Масштабирование вычислений глубокого обучения путем увеличения аппаратных часов или количества микросхем является проблематичным в долгосрочной перспективе. Поскольку оно подразумевает, что затраты масштабируются примерно с той же скоростью, что и увеличение вычислительной мощности, а это быстро сделает дальнейший рост невозможным.

Будущее

Печальный вывод из вышесказанного.

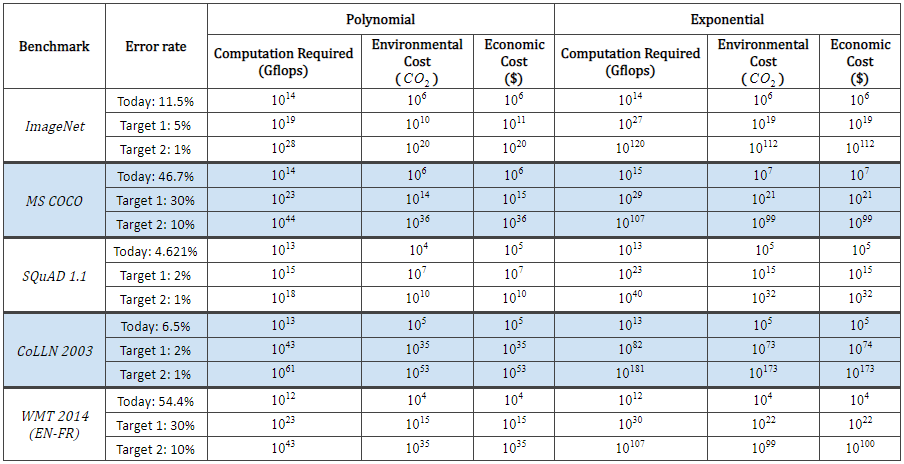
Следующая таблица показывает, какая вычислительная мощность и стоимость системы позволит достичь определенных целей в задачах ML, если экстраполировать текущие модели.

Задачи машинного обучения будут запускаться на самых мощных суперкомпьютерах.

Авторы научной работы считают, что требования для поставленных целей не будут выполнены. Хотя они рассматривают теоретически возможные варианты их достижения: улучшение эффективности без увеличения производительности, аппаратные ускорители типа TPU и FPGA, нейроморфные вычисления, квантовые вычисления и прочие, но ни одна из этих технологий (пока) не позволяет преодолеть вычислительные пределы ML.

Вывод

Уже в ближайшем будущем компьютерная производительность станет реальным барьером для улучшения эффективности множества задач машинного обучения по текущей траектории прогресса.