Условие
В компании «Мурзик и котята» резко упали регистрации на сайте. У аналитика появилась гипотеза, как повысить конверсию, и он решил проверить ее с помощью А/В-теста. Первая версия (контрольная) осталась без изменений, а во вторую (экспериментальную) добавили фотографии котят.

Спустя месяц аналитик собрал результаты. Старую версию сайта посетили 3 425 человек, из них 45 прошли регистрацию. На новой версии побывали 3 398 человек, зарегистрировались 64. Порог значимости стандартный — 5%.
Теперь аналитику нужно понять, о чем говорят эти цифры. С их помощью он сможет принять решение, которое повысит регистрации на сайте.
Задача
Помогите аналитику решить, сработала гипотеза или нет. Для этого нужно определить, является ли разница результатов статистически значимой.
Статистическая значимость — это математическая оценка того, насколько маловероятно, что наблюдаемая разница между группами получилась случайно, если на самом деле между ними нет никакого эффекта.
Решение
Первым делом необходимо вычислить конверсию каждой версии по формуле:
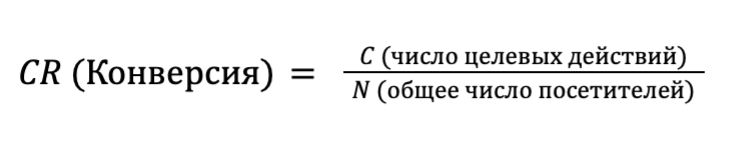
Определяем контрольную версию:
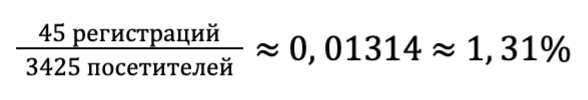
Определяем экспериментальную:
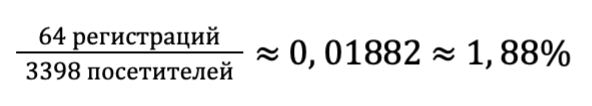
Разница конверсий — 0,57%. Кажется, что немало, но достаточно ли, чтобы считать ее статистически значимой? Давайте узнаем.
Чтобы вычислить, является ли эта разница статистически значимой, необходимо рассчитать три показателя: стандартную ошибку, Z-значение и P-value.
Стандартная ошибка (SE)
Позволяет оценить, насколько сильно могли бы колебаться наши результаты из-за случайности. Рассчитывается по формуле:
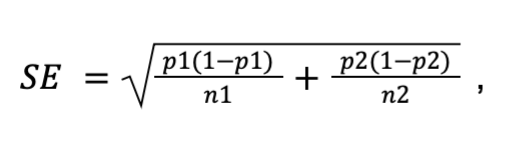
где p1 и p2 — конверсия двух групп, а n1 и n2 — размеры групп.
Вычислим значение стандартной ошибки для нашего условия:
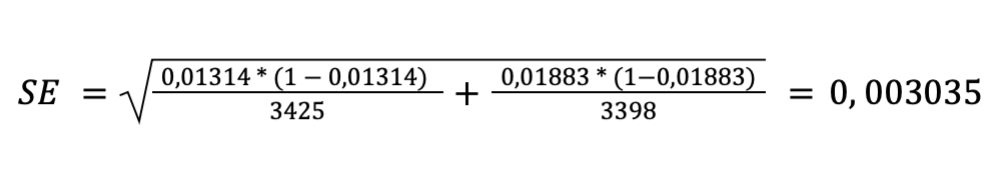
Это означает, что если бы версии сайта ничем не отличались, то результаты могли бы расходиться на 0,3% из-за случайности.
Наша разница — 0,57%. Результат больше стандартной ошибки, но это еще не доказывает, что он статистически значим.
Z-значение
Показывает, насколько далеко наблюдаемая разница отклоняется от нуля в стандартных отклонениях, то есть насколько она не случайна.
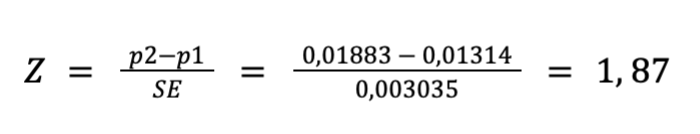
Значение показывает, что разница отличается от стандартной ошибки в 1,87 раз. Этого недостаточно для вывода, но достаточно, чтобы рассчитать следующий показатель.
P-value
Показывает, насколько вероятно получить разницу случайно, если на самом деле эффекта нет. Чем ниже значение, тем больше вероятность, что результат статистически значимый.
Чтобы вычислить показатель, воспользуемся таблицей нормального распределения и результатом Z-значения. 1,87 состоит из суммы чисел 1,8 и 0,07. По вертикальной оси отмечаем 1.8, а по горизонтальной — 0,07. Нужное число находится на пересечении.

С помощью таблицы мы получили 09693. Это значит, что если бы между версиями сайта не было никакой разницы, то шанс получить результат менее заметный, чем наш (0,57%), составляет 96,93%.
Теперь можем вычислить вероятность того, что текущий результат не случайный. Для этого вычитаем предыдущее значение из 100%.
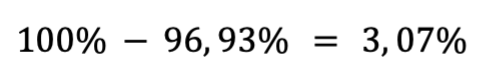
Нас интересуют любые отклонения как в одну сторону (новая версия лучше), так и в другую (новая версия хуже). Для этого проводим двусторонний тест и умножаем вероятность на два.
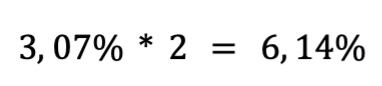
Это и есть наше p-value — вероятность получить такую разницу (или большую), если на самом деле никакой разницы нет. Получается, есть 6.14% шанс, что такие результаты могли получиться случайно, просто из-за разброса.
Далее сравниваем показатель с порогом значимости, который был установлен аналитиком при проведении A/B-теста (5%).
Ответ и заключение
6,14% > 5%. Это значит, что результат статистически не значим, хоть и близок к этому. Аналитику следует продолжить тестирование и собрать больше результатов или сделать вывод о том, что гипотеза не сработала и фотографии котиков не повысили конверсию в регистрацию.
Если же p-value будет равен или меньше порога значимости, тогда результаты станут статистически значимыми. Такую гипотезу можно смело воплощать в жизнь.